144. Binary Tree Preorder Traversal #

Problem #

Given the root of a binary tree, return the preorder traversal of its nodes’ values.

Example #

Example 1: #

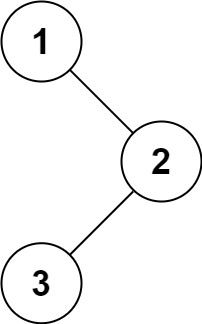
Input: root = [1,null,2,3]

Output: [1,2,3]

Constraints #

• The number of nodes in the tree is in the range [0, 100].
• 100 <= Node.val <= 100

Follow up #

Recursive solution is trivial, could you do it iteratively?

Approach and Intuition #

Recursive approach #

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }

    public void helper(TreeNode root, List<Integer> res) {
        if (root != null) {
            res.add(root.val);
            helper(root.left, res);
            helper(root.right, res);
        }
    }
}

Complexity Analysis #

Time complexity: \( O(n) \) as the recurrence relation is \( T(n) = 2T(n/2) + 1 \) .

Explanation #

Recurrence Relation:

Let \(T(n)\) is the number of operations executed in your traversal algorithm(DFS). Function is recursively called 2 times each time for left and right sub-tree.

\( T(n) = 2T(n/2) + 1 \) .

Using the Masters’ Theorem , we have
\(T(n) = a*T(n/b) + f(n)\)

f(n) is some constant.

For a Graph, the complexity of a Depth First Traversal is \( O(V + E) \) , where V is the number of nodes or vertices, and E is the number of edges.

A Binary Tree is also a Graph, and we visit each node only once.

The complexity of each of these Depth-first traversals(Pre, In and Post) is \(O(V + E)\) or \(O(N + E)\) .

Since the number of edges that can originate from a node is limited to 2 in the case of a Binary Tree, the maximum number of edges in a Binary Tree is \(n-1\) , where n is the total number of nodes.

The complexity then becomes \(O(n + n-1)\) , which is \(O(n)\) .

As for recursion, the only difference is that recursive method calls build the stack implicitly by pushing call frames to the JVM stack

Master Theorem #

Let \(T(n)\) be a monotonically increasing function that satisfies:

\(T(n) = a T(n/b) + f(n)\)
\(T(1) = c\)

where \(a >= 1, b >= 2, c>0\) .

If \(f(n)\) is \(\Theta(n^d)\) where \(d >= 0\)
then

\( x = \begin{cases} a &\text{if } b \\ c &\text{if } d \end{cases} \)

Space Complexity: \( O(1) \)

Iterative #